What does LBM actually solve?
Learn why it is used for fluid flow problems
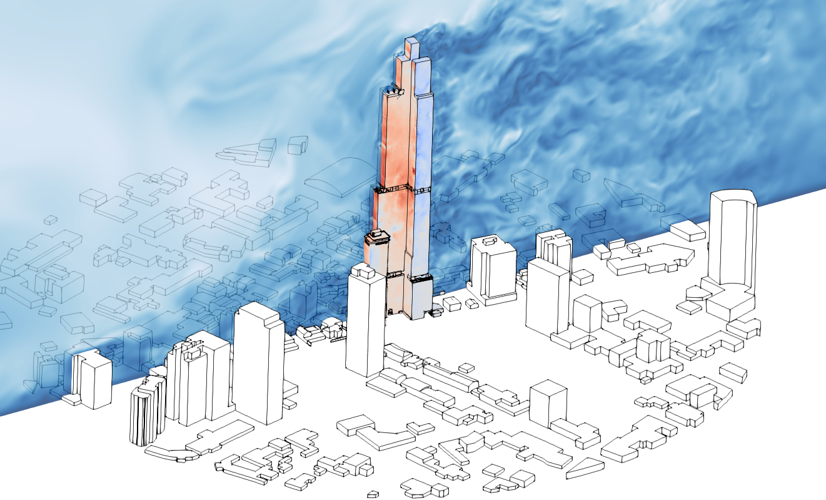
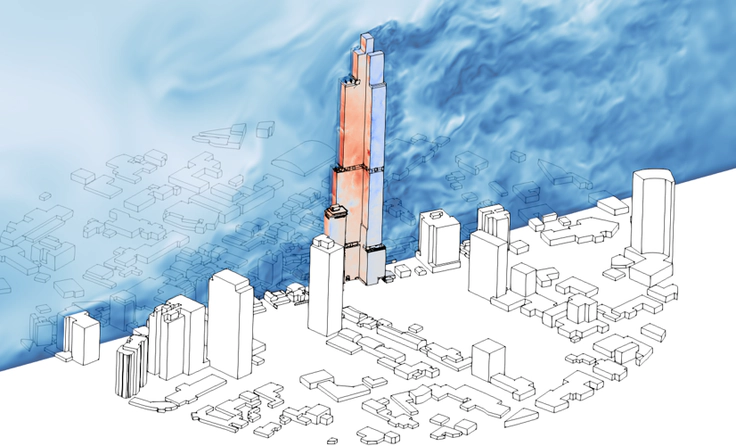 Wind flow simulation with LBM
Wind flow simulation with LBMIf you work with computational fluid dynamics (CFD), you’ve certainly heard of LBM – the Lattice Boltzmann Method. LBM is becoming increasingly popular as more professionals discover new use cases and take advantage of the greater productivity it can offer. Although it has existed for several decades, the industrial adoption of LBM is relatively recent. As a result, many people still believe that the method solves “particle collisions” (which is not true). This article will explain the most fundamental concepts you need to know about LBM and how it can benefit your projects.
What is the equation solved in LBM?
The theory of LBM originates from gas kinetics, where, through modeling collisions between gas molecules and their velocity distributions, it is possible to deduce macroscopic fluid properties such as temperature and viscosity. The main equation in kinetic theory is the Boltzmann equation, which describes the behavior of populations of microscopic particles in phase space:
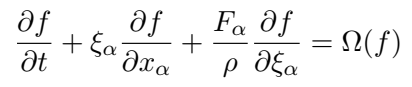
Boltzmann equation
The Boltzmann equation can be understood as a mesoscopic description of the kinetic problem of molecules, as it does not represent individual molecules but rather the probability distribution of particles moving in a certain direction having a certain mass and velocity (this is what we call populations).
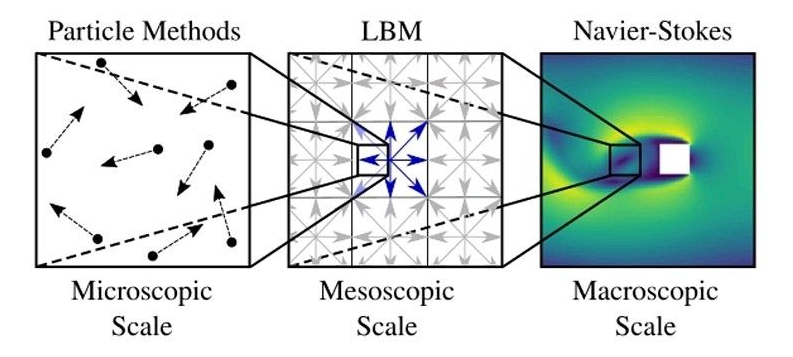
Source: Suraj Thakur.
What does the method solve at macroscopic scale?
In mesoscopic modeling, moments of the populations ($$f$$) can be defined, which are integrations over all velocity directions, and these moments can be given specific meanings. For example, we know that the following moments represent the density and velocity of a fluid:
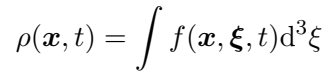
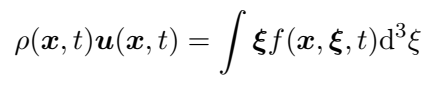
But how do we know this? We understand the meaning of the moments by verifying which macroscopic equation the lattice Boltzmann equation is equivalent to. The most well-known method for performing this verification is the Chapman-Enskog analysis, which derives the macroscopic expressions for each type of moment you might want to generate from $$f$$. You’re probably eager to learn every detail of this procedure, and for that, I suggest reading Krüger et al, The lattice Boltzmann method: Principles and Practice, Chapter 4. Now, let’s get to the point. Using the moments defined above, the equivalent macroscopic equations are:
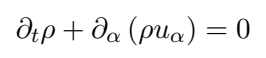
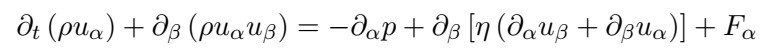
Don’t they look familiar to something you know? The lattice Boltzmann equation effectively represents the weakly compressible Navier-Stokes equations, provided certain relationships between the mesoscopic and macroscopic properties are satisfied.
What if I want to run an incompressible case?
In LBM, the Mach number is defined by the choice of the mesoscopic velocity value ($$u$$). Since the speed of sound is constant, to simulate incompressible flows, you simply need to keep the Mach number low, preferably less than 0.1.
Why solve Navier-Stokes this way?
If we already have a well-established method for solving fluid motion, the finite volume method, you may wonder why we need a new method. The main reason that attracts so many people to LBM is its fantastic computational performance. This performance is explained by the locality of its algorithm. The time integration of the method is a simple explicit forward Euler, converted to second order through a change of variables. The solution of the Boltzmann equation is commonly separated into the following main processes (simplified for the sake of brevity):
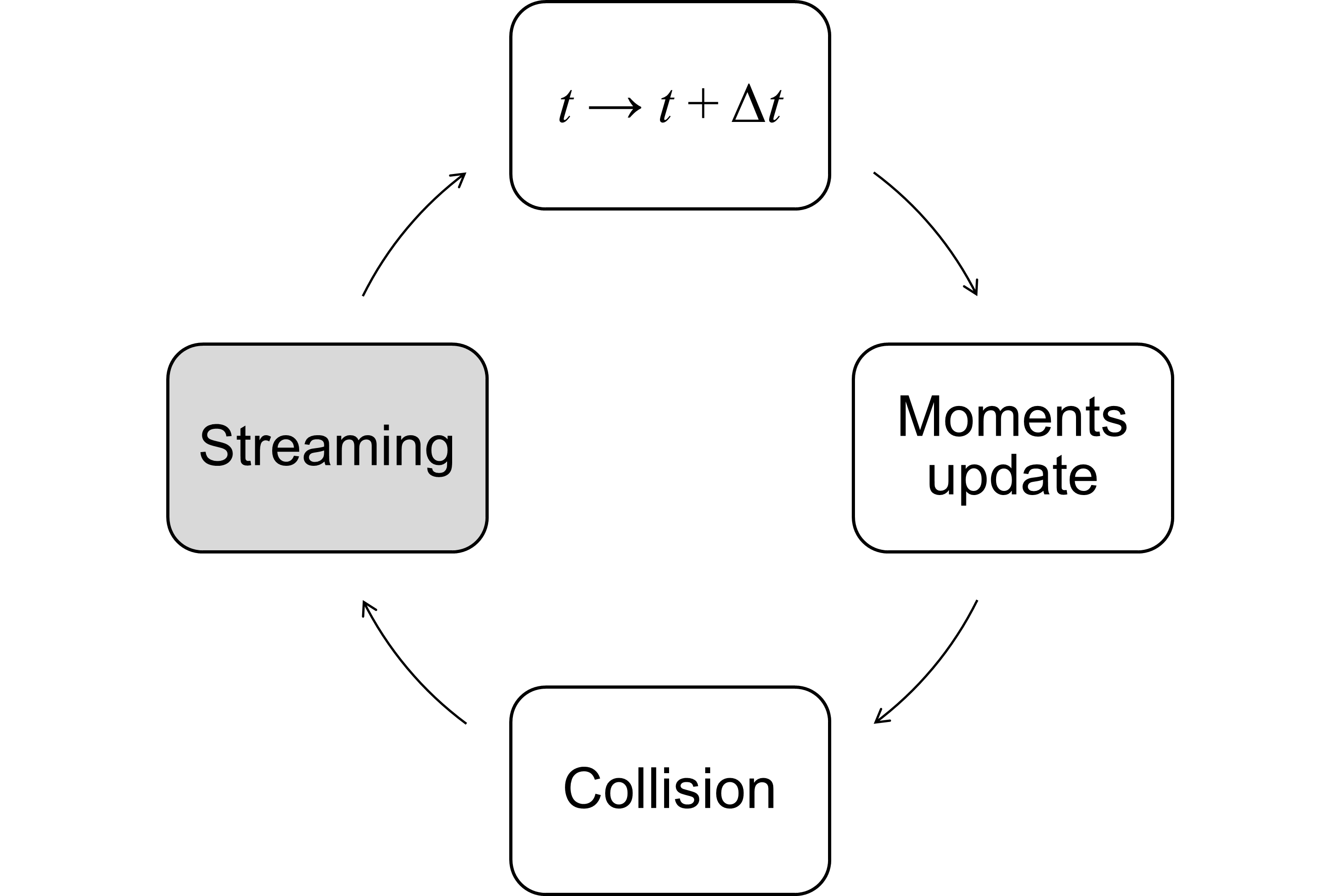
Of these processes, only the streaming is not a local operation. This high amount of local operations makes the algorithm’s performance in parallel computing exceptional. Furthermore, the calculation of strain rates can also be done locally, eliminating the need for gradients.
To give you an idea of performance, the CFD software AeroSim, for example, has a typical measure of 500 MNUPS (million nodes updated per second) on an Nvidia V100 GPU. This means that every second of wall time, 500 million mesh elements are updated! On a mesh with 100 million elements, which is considered a sufficient magnitude for urban microclimate problems, 5 time steps are advanced per second. In this case, a transient simulation of several minutes of sampling (real scale) can be completed in just a few hours, at a machine cost much lower than that of large CPU clusters.
Summary
For a long time, some misconceptions about LBM have been spread. This text helps demystify some of these prejudices and clarifies why LBM is becoming so popular so quickly. Time is money, especially in our field of CFD. Through the high computational performance of LBM, the CFD engineer can impact their organization with shorter project cycles, and their society with higher-quality products.
The LBM method evolves alongside the advancement of GPUs, as its performance is directly tied to two computational aspects:
- processing speed and
- hardware memory capacity.
The rise of artificial intelligence has significantly driven GPU development, and LBM has benefited from this trend. In the future, LBM is expected to continue gaining more applications in real-world engineering problems.
In the next articles, we are going to show how simple it is to create a computational mesh in LBM, and give real world examples of wind engineering problems that have been successfully solved with LBM simulations.

Alan Lugarini
Alan is a computational fluid dynamics (CFD) scientist specializing in turbulence simulation techniques for wind actions.
